JELoWeb

Home Page

MinPins

Misc Photos

Jeep Events

2002 Jeep Wrangler

House Photos

Garage Addition

Masters Thesis

SouthWest Pacific Photos

Antarctic Trip

Having assembled the available seismicity data and selected appropriate events, the next step is to proceed with the fault rupture and slip modeling. These concepts will be developed in the following sections.

As mentioned earlier, using a circular fault model, estimates of both the fault rupture area and average displacement over the rupture can be calculated given the event moment, an assumed average stress drop and selected parameters describing the physical properties of the plate material involved. The seismic moment is given by (Lay and Wallace, 1995, p. 388):

This relationship states that the moment, , is equal to the product of the shear modulus or plate rigidity, m , the fault rupture area, A, and the average displacement or slip on the fault, . Assuming a circular fault model, the fault area A becomes where is now the radius of the fault rupture area. Substitution into the above gives:

The moment relationship for stress drop on a circular fault rupture is given as (Lay and Wallace, 1995, p. 377; Scholz, 1990, p. 182):

Where: is again the moment, D s is the average stress drop in the earthquake, and is again the radius of the fault rupture area. These, then, are the standard equations for a circular fault rupture model. Equating the two preceding equations and solving for the radius of the fault rupture area gives:

Then the average displacement over the ruptured fault area is:

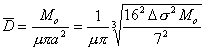
These expressions give the slip and rupture area in terms of the measured quantity , the average stress drop, , and plate rigidity, . Estimation of stress drop and plate rigidity are described in later sections.

To model the individual event fault ruptures and slips it is necessary to have moment values for all earthquakes. The HCMT catalog and Chinn and Isacks provide estimates of event scalar moments. For events from Abe's catalog, more traditional magnitude estimates are given and therefore event moments must be determined. No direct magnitude-moment relationships exist but empirical relationships have been developed for this conversion. Where surface wave magnitude, Ms, is available, event moment can be calculated as (Kanamori, 1983):

Where the body wave magnitude, mB, is available, event moment can be calculated as (Kanamori, 1983):

Using these relationships moments for events without published moment estimates were calculated. Where both surface wave magnitude, Ms, and body wave magnitude, mB, were available, moments calculated using Ms were preferred.

The selected events from the sources exhibit moments ranging from 3.58 x 1023 through 8.91 x 1027 dyne-cm. A detailed break down of event moment ranges is given in table 5. For comparison purposes, all event classifications have been included in the table. It can be seen that Abe's catalog contains large to great events, and larger shallow events in the HCMT catalog are predominantly reverse in nature.

Table 5. Event moment breakdown with all duplicated events removed.

On a related note, periodically values for the moment magnitude, Mw, are used for comparison or in calculations. Mw is defined by (Kanamori 1983):

The fault rupture and slip equations require selection of a few additional parameters to complete the calculations. These are: m , the modulus of rigidity, and D s , the earthquake average stress drop. Cloos (1992) mentions the modulus of rigidity, m , for plates is generally considered to be between 2 to 10 x 1011 dyne/cm2. Pacheco (1993), in his broad based study of subduction zones, has used an average value of 5 x 1011 dyne/cm2. For comparison, Lay and Wallace (1995, p. 51) give the rigidity of olivine, a major mineral component of oceanic plates, to be 8.2 x 1011 dyne/cm2. For calculations here, the median value of 5 x 1011 dyne/cm2 as used by Pacheco will be used.

The classic study of earthquakes by Hanks (1977) reveals the average stress drop is independent of event size but may vary somewhat with type of earthquake. In this study, Hanks estimated event source radii for nearly 400 earthquakes by scaling spectral parameters of the far-field double-couple point source model of Brune (1970, 1971) to correlate with observed body-wave spectra, then plotting moment and radius in log-log form (see figure 9). The source model used by Hanks has been shown to successfully explain both near- and far-field spectra observed for earthquakes (Brune 1970). Hanks' results clearly show a linear trend in the grouping of events with most falling within a range of

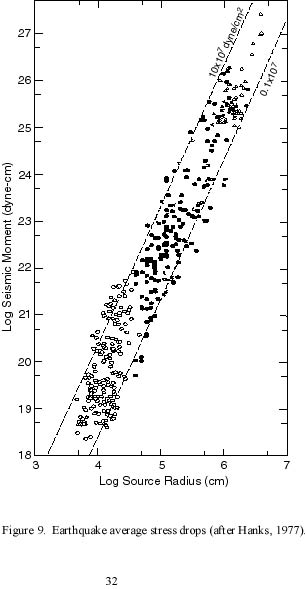
stress drop from .03 to 30 x 107 dyne/cm2. The mean stress drop for this range is approximately 3 x 107 dyne/cm2. Currently lacking evidence that stress drops for events along the New Hebrides Trench are anything other than average, the event average stress drop is most likely in the range of the mean average stress drop mentioned above and this value will be used in the calculations that follow.

Cloos (1992) has presented some relations between earthquake parameters and event size. For comparison, the values calculated are compared with the relationships determined by Cloos in figure 10.

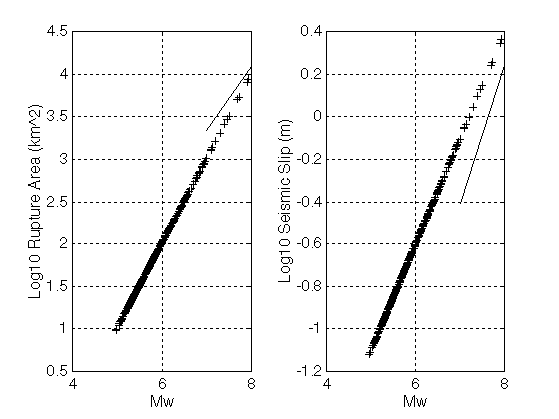
Figure 10. Comparison of average stress drops. Solid lines represent linear best-fit of Cloos (1992) over the range of events he considered. Symbols represent values for events calculated here.

The rupture area and seismic slip values calculated for the events here show reasonable agreement with the relationships determined by Cloos but vary by a factor of roughly two. Slight variations in the assumed average stress drop can cause a similar variation in the results of the calculations here.

Finally, having selected the appropriate events, calculated the necessary moments, and chosen the required parameters, the event fault rupture areas and average slips can be calculated. Table 6 shows some sample events and the resulting parameters calculated using the equations developed here.

Table 6. Example calculations of fault radius and slip.

The 13 July, 1994, example calculation shown in the table above is given for comparison purposes. Calmant et al. (1997) in a detailed analysis of this event gives the fault area as 63 by 21 kilometers and the slip as 163 centimeters. These dimensions give a rupture area of 1323 square kilometers. This is equivalent to a circular fault having a radius of 20.5 km which is in good agreement with the modeled radius of 21.3 km in the example calculation. The slip, however, is somewhat different. This difference, 163 centimeters versus 93 centimeters calculated here, may be due to the fact that this event was a shallow dipping (42° ) primarily left-lateral strike-slip earthquake associated with faulting within the upper plate. This appears consistent with the idea that intraplate earthquakes have higher average stress drops than same size interplate events (Scholz et al., 1986). (Recall, in the circular fault rupture model equations, an increase in the selected value of average stress drop, D s , leads to an increase in average slip, , and a smaller decrease in fault radius, .) Incidentally, this event being a strike-slip event is included here only for comparison and was not included in the slip determination calculations. Only reverse dip-slip events as determined using the methods of Frohlich and Apperson (1992) are used for this purpose.

To properly accumulate slip from these events requires consideration of the three-dimensional nature of this problem. Taking the view of Cloos (1992), and Cloos and Shreve (1996), thrust events along subduction zones primarily involve the rupture of asperities within a subduction channel between the subducting and overriding plates. In this view then, these surfaces are not planar but uneven and irregular by nature. However, considering all slip to be on a fault 'plane' lends simplification to conceptualizing the problem and the eventual calculations. If we further assume, at least for the moment, that plate convergence at the subduction zone is not oblique, projecting nearby but out-of-plane fault ruptures along trench normals onto the fault plane can allow accumulation of overlapping ruptures and slips within a two-dimensional space. The details of the process of geometrically projecting the event epicenters to the fault plane is given in appendix A1. Figures 11 and 12 show the data sets in this trench-normal

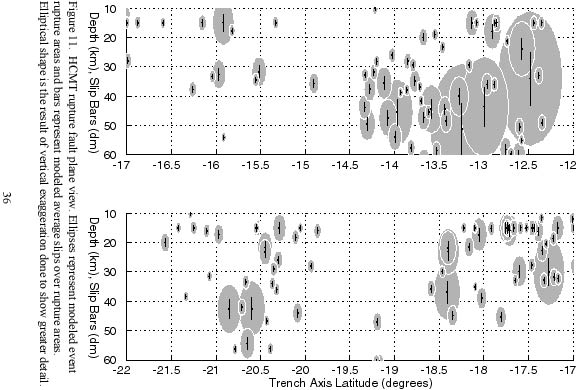
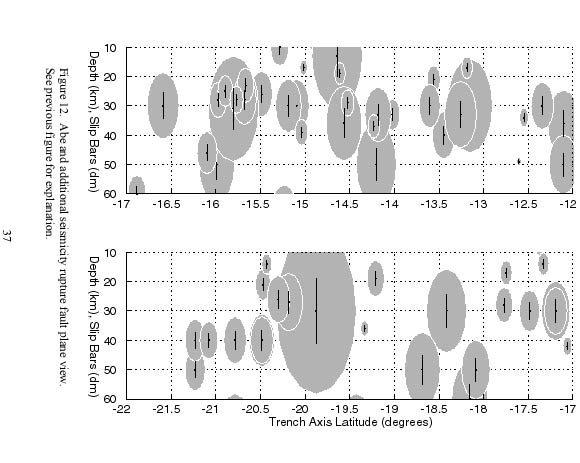
projected fault plane view. Although, actual reverse earthquake ruptures often have complex slip histories with variable slip over the fault plane, the simplified depiction of earthquakes as circular ruptures with the hypocenter at the center is consistent with the point source circular rupture assumptions of the CMT method and equations chosen for earthquake rupture modeling.

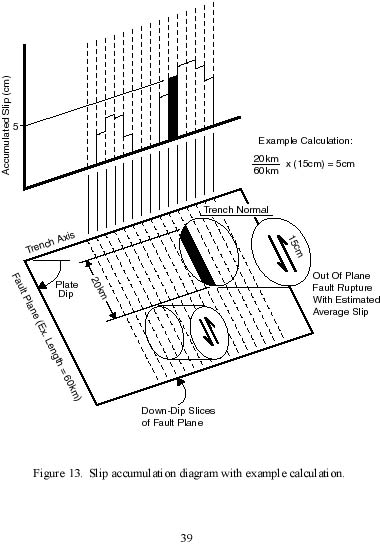
Recall the circular fault modeling here estimates the average slip over a rupture area. The circle represents the rupture area but we have yet to account for the slip within the area. To do this, first we divide the fault plane into down-dip slices from the surface to depth (see figure 13). Then, taking the length of the down-dip slice of the fault plane covered by the portion of the event fault rupture circle, dividing that by the down-dip extent of the fault plane, and then multiplying by the average slip during the event gives the average down-dip slip along the fault plane (see example calculation included in figure 13). Overlapping fault rupture circles simply have their individually calculated average slips summed to generate the accumulated average slip. This is also carried across the different data sets to arrive at the total accumulated average seismic slip. Lastly, this total is divided by the duration of the seismic data sources (beginning of 1900 through the end of 1997 or 98 years) to get the average annual down-dip seismic slip.

Several parameters must be chosen to complete the calculations in this section. These include the maximum depth of coupling (or the down-dip length of the fault plane) and the fault plane slice width. Chinn and Isacks (1983) suggest the depth of coupling along the New Hebrides Trench is in the range of 35 to 50

kilometers. Pacheco et al. (1993) have used 45 kilometers as the limiting depth for their comparative investigation of 19 subduction zones. However, the HCMT data used here shows clustering of near-trench reverse seismicity to depths approaching 70 kilometers (see figure 5). For this reason, a compromise maximum depth of 60 kilometers will be used for the depth of coupling in the calculations. Also, since trench depths can reach to 6.5 kilometers and HCMT solutions are already constrained to depths of 10 kilometers or greater, an upper limit is also chosen at 10 kilometers depth. Coincidentally, this same upper limit is chosen by Pacheco et al. (1993) in their investigation, although their reasons differ slightly.

In accumulation of the average slips, some of the fault rupture circles extend shallower than the 10 kilometer minimum depth or deeper than the 60 kilometer maximum depth of coupling. However, all of the slip from the fault ruptures was accounted for and averaged over the 50 kilometer down-dip fault plane length. In other words, all slip for a given event was treated as if it occurred within the 10 to 60 kilometer depth range limits regardless of whether the geometrical representation of the fault rupture circle fit entirely within this range (refer to figures 11 and 12).

Variations in the selected down-dip length of the fault plane result in variations in the seismic coupling estimate. Shortening the down-dip length works to increase the effective slip while lengthening decreases it. For example, shortening the down-dip fault plane length by 10 kilometers to 40 kilometers increases the average annualized slip by 25%. Increasing the down-dip fault plane length by 10 kilometers to 60 kilometers decreases the average annualized slip by 16.7%.

Lastly, to provide a fine enough resolution to capture small and large events, a fault plane slice width of 0.01 degrees latitude (100 slices per degree of latitude) was chosen. Figure 14 shows the average annual seismic slip along the subduction zone. A sliding average with a window of two degrees of latitude is also included.

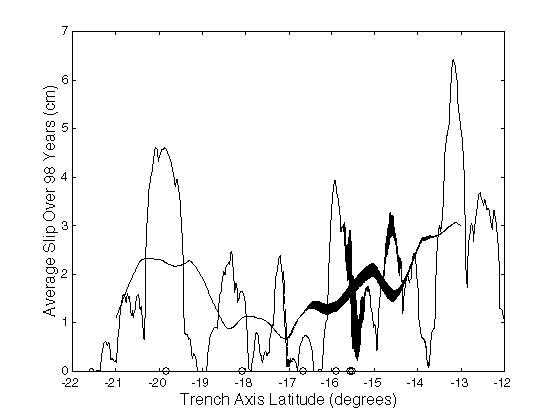
Figure 14. Annualized accumulated and smoothed seismic slip. More variable line is annualized accumulated seismic slip. Smoothed line is the sliding average value of the annualized accumulated seismic slip using a window of 2° latitude. Dark areas represent the possible additional slip accommodation in the back-arc region. Circles along the trench axis show the relative locations of the GPS sites.

© jlundy@wyoming.com 20 June 2003